

Answer: D
Solution:
It will take him 300*2=600 seconds to paint all the dimples. This is equivalent to 600/60=10 minutes .
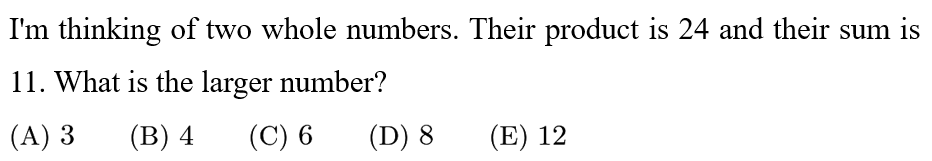
Answer: D
Solution:
Let the numbers be x and y. Then we have x+y=11 and x*y=24. Solving it , one is 3,the other is 8.
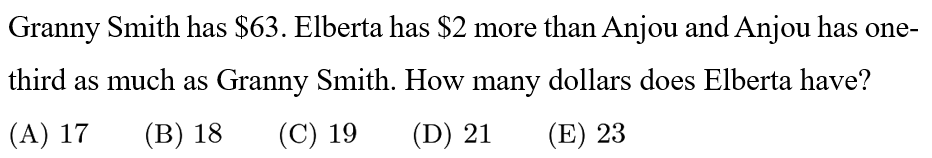
Answer: D
Solution:
Since Anjou has 1/3 the amount of money as Granny Smith and Granny Smith has $63, Anjou has 63*1/3=21 dollars. Elberta has $2 more than this, so she has $23.

Answer: E
Solution:
Since the number is even, the last digit must be 2 or 4. To make the smallest possible number, the ten-thousands digit must be as small as possible, so the ten-thousands digit is 1. Simillarly, the thousands digit has second priority, so it must also be as small as possible once the ten-thousands digit is decided, so the thousands digit is 2. Similarly, the hundreds digit needs to be the next smallest number, so it is 3. However, for the tens digit, we can't use 4, since we already used 2 and the number must be even, so the units digit must be 4 and the tens digit is 9 (The number is 12394.)

Answer: C
Solution:
During those 10 seconds, the sound traveled 1088*10=10880 feet from the lightning to Snoopy. This is equivalent to 10880/5280=2 miles.

Answer: B
Solution:
There are 3 spaces between the 1st and 4th trees, so each of these spaces has 60/3=20 feet. Between the first and last trees there are 5 spaces, so the distance between them is 20*5=100 feet.


Answer: A
Solution:
The area of a kite is half the product of its diagonals. The diagonals have lengths of 6 and 7, so the area is 6*7/2=21.

Answer: E
Solution:
Each diagonal of the large kite is 3 times the length of the corresponding diagonal of the short kite since it was made with a grid 3 times as long in each direction. The diagonals of the small kite are 6 , 7, so the diagonals of the large kite are 18, 21. and the amount of bracing Genevieve needs is the sum of these lengths, which is 39.

Answer: D
Solution:
The large grid has dimensions three times that of the small grid, so its dimensions are 18*21, The area of the kite is half the product of its diagonals: 18*21/2=189. Thus, the area of the remaining gold is 18*21-189=189.
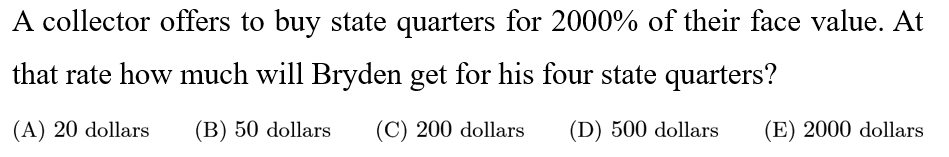
Answer: A
Solution:
2000% is equivalent to 20*100%. Therefore, 2000% of a number is the same as 20 times that number. 4 quarters is 1 dollar, so Bryden will get 20*1=20 dollars.

Answer: C
Solution:
The area of a trapezoid is : 1/2*(2+4)*6=18.
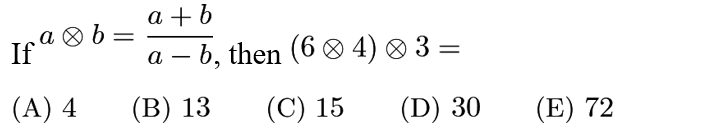
Answer: A
Solution:
6@4=(b+4)/(6-4)=10/2=5; 5@3=(5+3)/(5-3)=8/2=4;
Answer: D
Solution:
There are 36 students in the class: 12 prefer chocolate pie, 8 prefer apple pie, and 6 prefer blueberry pie. Therefore, 26-12-8-6=10 students prefer cherry pie or lemon pie. Half of these prefer each, so 5 students prefer cherry pie. This means that 5/36 of the students prefer cherry pie, so 5/36 of the full 360 should be used for cherry pie. This is 50.

Answer: C
Solution:
There are 3 possibilities for the meat and 4 possibilites for the dessert, for a total of 4*3=12 possibilities for the meat and the dessert. There are 4 possibilities for the first vegetable and 3 possibilities for the second, but order doesn't matter, so we overcounted by a factor of 2. so the total possibilites for the two vegetables is 4*3/2=6, and the total number of possibilites is 12*6=72.

Answer: A
Solution:
After the 4 minutes of Homer peeling alone, he had peeled 4*3=12 potatoes. This means that there are 44-12=32 potatoes left. Once Christen joins him, the two are peeling potatoes at a rate of 3+5=8 potatoes per minute. So, they finish peeling after another 32/8=4 minutes. In these 4 minutes, Christen peeled 4*5=20 potatoes.

Answer: E
Solution:
The smaller rectangles each have the same height as the original square, but have 1/4 the length, since the paper is folded in half and then cut in half the same way. The larger rectangle has the same height as the original square but has 1/2 the length, since the paper is cut in half after the fold but the fold retains both sides of the larger rectangle. Therefore, the smaller rectangles have dimensions 4*1 and the larger rectangle has dimensions 4*2. The ratio of their perimeters is (2*(4+1))/(2*(4+2))=5/6.

Answer: B
Solution:
Notice that in two of the increases, the dollar amount doubles. The increases in which this is not true is 2 to 3, 3 to 4 , 11 to 12. We can disregard 11 to 12 since that increase is almost 2 times. The increase from 2 to 3 is (300-200)/200=1/2, so it's only multiplied by a factor of 1.5. The increase from 3 to 4 is (500-300)/300=2/3, so it's only multiplied by a factor of 1.6. Therefore, the smallest percent increase is From 2 to 3.

Answer: D
Solution:
This is equivalent to asking for the probability that at least one of the numbers is a multiple of 5, he probability of not rolling a 5 on either dice is C(6,5)*C(6,5)=25/36. . Therefore, the probability of rolling at least one five, and thus rolling two numbers whose product is a multiple of 5, is 1-25/36=11/26.

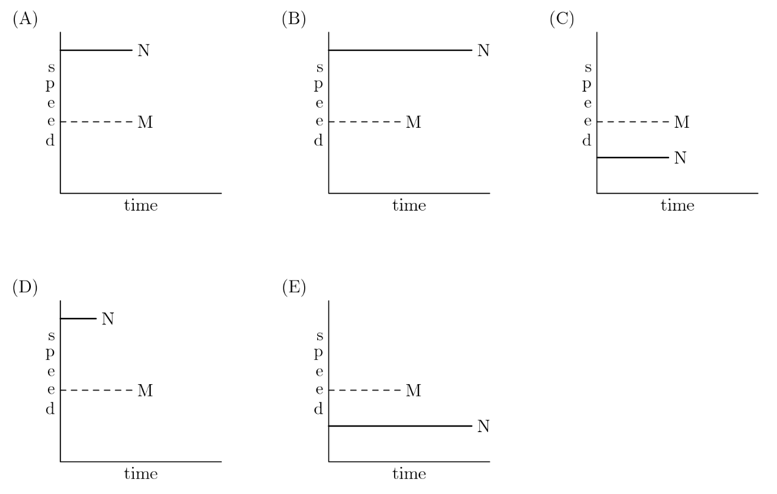
Answer: D
Solution:
Since Car N goes at a faster speed than Car M, it will take less time to get to the same destination. Reviewing the graphs, we see that only one graph fits this criteria, graph D.

Answer: A
Solution:
Since the only other score Quay knows is Kaleana's, and he knows that two of them have the same score, Quay and Kaleana must have the same score, and K=Q. Marty knows that he didn't get the lowest score, and the only other score he knows is Kaleana's, so Marty must know that Kaleana must have a lower score than him, and M>K. Finally, Shana knows that she didn't get the highest score, and the only other score she knows is Kaleana's, so Shana must know that Kaleana must have a higher score than her, and S<K. we have S<Q<M.

Answer: D
Solution:
Since there is an odd number of terms, the median is the number in the middle, specifically, the third largest number is 18, and there are 2 numbers less than 18, 2 numbers greater than 18. The sum of these integers is 5*15=75, since the mean is 15. To make the largest possible number with a given sum, the other numbers must be as small as possible. The two numbers less than 18 must be positive and distinct, so the smallest possible numbers for these are 1 and 2. The number right after 18 also needs to be as small as possible, so it must be 19. This means that the remaining number, the maximum possible value for a number in the set, is 75-1-2-18-19=35.

Answer: E
Solution:
The highest possible score is if you get every answer right, to get 5*20=100. The second highest possible score is if you get 19 questions right and leave the remaining one blank, to get a 5*19+1=96. Therefore, no score between 96 and 100, exclusive, is possible, so 97 is not possible.

Answer: D
Solution:
we see that we can split this equilateral dot triangle to two halves. Using the smaller triangle we won't have to worry about extra unneeded cases. We can see that there are three distinct triangles in the half, and combining this with the larger equilateral triangle our answer is 3+1=4.

Answer: B
Solution:
There are 2 pairs of red triangles, 3 pairs of blue triangles, so leaving 1 red triangle, 2 blue triangles, and 8 white triangles remaining on each half. Also, we have 2 red-white pairs. we must use 1 red triangle and 1 white triangle per side, leaving 2 blue triangles and 7 white triangles apiece. The remaining blue triangles cannot be matched with other blue triangles, so the remaining blue triangles must be paired with white triangles. This uses 2 blue triangles and 2 white triangles on each side, leaving 5 white triangles apiece, which must be paired with each other.

Answer: D
Solution:
The thousands digit of the smaller digit should be 2. The larger number could be 2 or 3 multiple of the smaller one.
2475*3=7425.
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,